11/10/2020 22:33
Ответ на задачу в задаче
Итак, решение задачи из предыдущего поста таково.
Для определения радиуса звезды используется закон излучения Стефана-Больцмана. Но этот закон дает нам полную мощность излучения звезды во всем диапазоне длин волн. В то же время в условии задачи приведена визуальная абсолютная звездная величина, которая учитывает только ту часть спектра, которая воспринимается человеческим глазом, да еще и адаптированная к спектральной чувствительности глаза. И если для звезд типа Солнца большая часть энергии излучается в этом диапазоне (странно, да? ;)), то для звезды с температурой фотосферы 21000K изрядная доля энергии будет излучаться в более коротковолновом диапазоне, нежели видимый свет. Поэтому для корректного применения формулы (2) (см. задачу) надо использовать не визуальные звездные величины Солнца и β Центавра, а так называемые болометрические, учитывающие излучение во всем спектре.
Болометрическую абсолютную величину Солнца 4,75 можно найти, например, в Википедии. Для β Центавра её придется вычислить по визуальной с помощью болометрической поправки. Теоретическое определение такой поправки не так просто и выполняется на основе модели атмосферы звезды. Поэтому поправка будет зависеть не только от температуры, но и от класса светимости. График такой поправки для звезд классов O3-M8 главной последовательности можно взять в работе [1]:
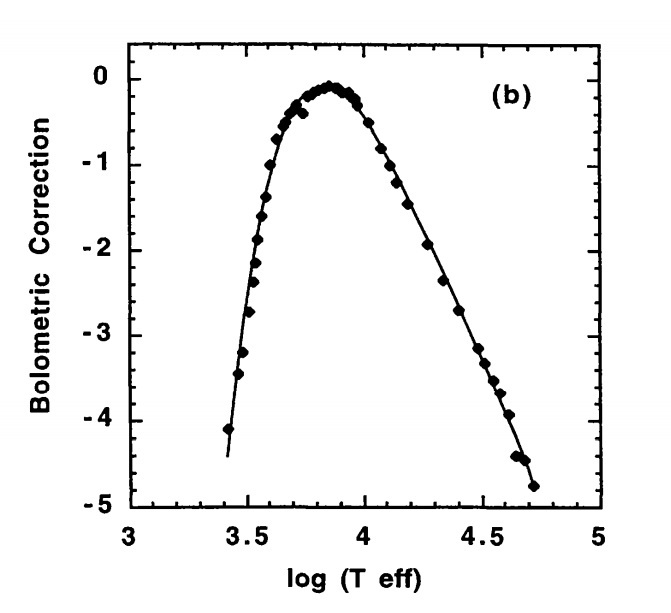
Для T=21000 получаем lg(T)=4,3, после чего по графику находим поправку BC=-2,1, а затем и болометрическую абсолютную звездную величину:

После этого применяем формулу (2):
}=2{,}512^{10{,}65}\approx%2018200.)
После чего формула (1) дает радиус звезды:

Это уже гораздо ближе к ответу из задачника. Различие в 0,5 зв. величины вызвано неточностью чтения болометрической поправки с графика, а так же тем, что Воронцов-Вельяминов использовал несколько другу аппроксимацию этой поправки и более точную температуру фотосферы Солнца.
1. Lang, Kenneth R. Astrophysical Data. I. Planets and Stars. Springer-Verlag Berlin Heidelberg New York (1992).
Для определения радиуса звезды используется закон излучения Стефана-Больцмана. Но этот закон дает нам полную мощность излучения звезды во всем диапазоне длин волн. В то же время в условии задачи приведена визуальная абсолютная звездная величина, которая учитывает только ту часть спектра, которая воспринимается человеческим глазом, да еще и адаптированная к спектральной чувствительности глаза. И если для звезд типа Солнца большая часть энергии излучается в этом диапазоне (странно, да? ;)), то для звезды с температурой фотосферы 21000K изрядная доля энергии будет излучаться в более коротковолновом диапазоне, нежели видимый свет. Поэтому для корректного применения формулы (2) (см. задачу) надо использовать не визуальные звездные величины Солнца и β Центавра, а так называемые болометрические, учитывающие излучение во всем спектре.
Болометрическую абсолютную величину Солнца 4,75 можно найти, например, в Википедии. Для β Центавра её придется вычислить по визуальной с помощью болометрической поправки. Теоретическое определение такой поправки не так просто и выполняется на основе модели атмосферы звезды. Поэтому поправка будет зависеть не только от температуры, но и от класса светимости. График такой поправки для звезд классов O3-M8 главной последовательности можно взять в работе [1]:

Для T=21000 получаем lg(T)=4,3, после чего по графику находим поправку BC=-2,1, а затем и болометрическую абсолютную звездную величину:
После этого применяем формулу (2):
После чего формула (1) дает радиус звезды:
Это уже гораздо ближе к ответу из задачника. Различие в 0,5 зв. величины вызвано неточностью чтения болометрической поправки с графика, а так же тем, что Воронцов-Вельяминов использовал несколько другу аппроксимацию этой поправки и более точную температуру фотосферы Солнца.
1. Lang, Kenneth R. Astrophysical Data. I. Planets and Stars. Springer-Verlag Berlin Heidelberg New York (1992).
Tags: